泄漏率 qL (mbar ·l · s–1)
根据上述定义,可以很容易地理解气体泄漏量(气体泄漏是指经由通道或“管道”发生的不应该的气体移动)也将以 mbar · l · s–1 作为表示单位。泄漏率通常是通过屏障一侧的大气压和另一侧的真空度 (p < 1 mbar) 来测量或表示。如果氦气(该气体可用作示踪气体等)在这些条件下通过泄漏穿过屏障,则称之为“标准氦气状况”,有关更多信息,请参阅检漏部分。
出气 (mbar · l)
术语“出气”是指气体和蒸汽从真空室壁或真空系统内部的其他组件中释放的现象。该气体量还以 p · V 的乘积来表征,其中 V 指气体释放至的容器的体积,p 或 Δp(最好使用后者表示)是指气体进入该体积所导致的压力增加。
出气率 (mbar · l · s–1)
这是指一段时间内的出气量,以 mbar · l · s–1 为表示单位。
出气率 (mbar · l · s–1 · cm–2)(相对于表面积)为了估计需要抽取的气体量,了解内部表面积的大小、材料和表面特性、相对于表面积的出气率及其随时间推移的变化情况非常重要。
分子的平均自由程 λ (cm) 和碰撞速率 z (s-1)
根据“气体由大量的不同颗粒构成,这些颗粒之间除了碰撞之外,相互不存在其他有效作用力”这一概念,人们进行了一系列的理论研究,如今这些研究均被纳入了“气体动理论”的范畴。
该理论得出的第一个也是最有用的结果之一就是能够利用气体密度、各种气体分子平均速度的平方 c2 以及分子质量 mT 来计算气体压力 p:
Leybold - Vacuum Fundamentals graphics
(1.14)
式中
Leybold - Vacuum Fundamentals graphics
(1.15)
气体分子会以各种可能的速度在相互之间飞行,并碰撞容器壁以及相互之间发生碰撞(弹性碰撞)。在气体动理论的帮助下,人们对气体分子的这种运动进行了量化描述。一个分子在给定时间段内的平均碰撞次数被称为碰撞指数 z,每个气体分子在与其他分子发生碰撞之间所飞行的平均路径距离被称为平均自由程长度 λ,该值可通过下式表示,由分子的平均速度 c、分子直径 2r 以及分子的颗粒数密度 n 进行描述 - 该公式可得出非常准确的近似值:
Leybold - Vacuum Fundamentals graphics
式中
Leybold - Vacuum Fundamentals graphics
(1.16)
以及
Leybold - Vacuum Fundamentals graphics
(1.18)
因此,根据方程 (1.1),颗粒数密度 n 的平均自由程长度 λ 与压力 p 成反比。因此,在恒定温度 T 下,每种气体都会遵循以下关系
λ ⋅ p = const (1.19)
(1.19)
λ ⋅ p = const (1.19)
表 3 和图 9.1 用于计算各种气体在任意压力下的平均自由程长度 λ。表 4 则汇总了对真空技术最为重要的一些气体分子运动方程式。
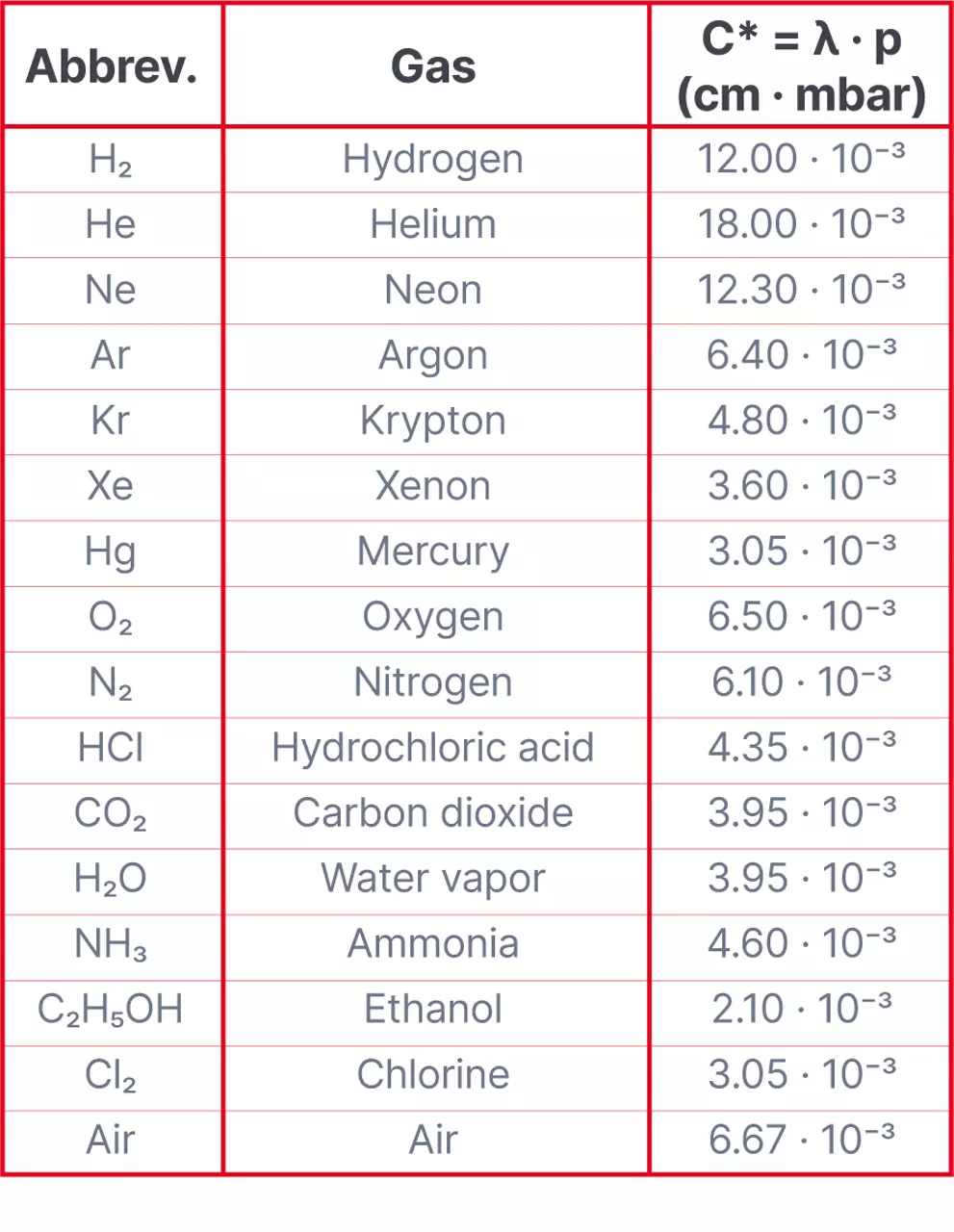
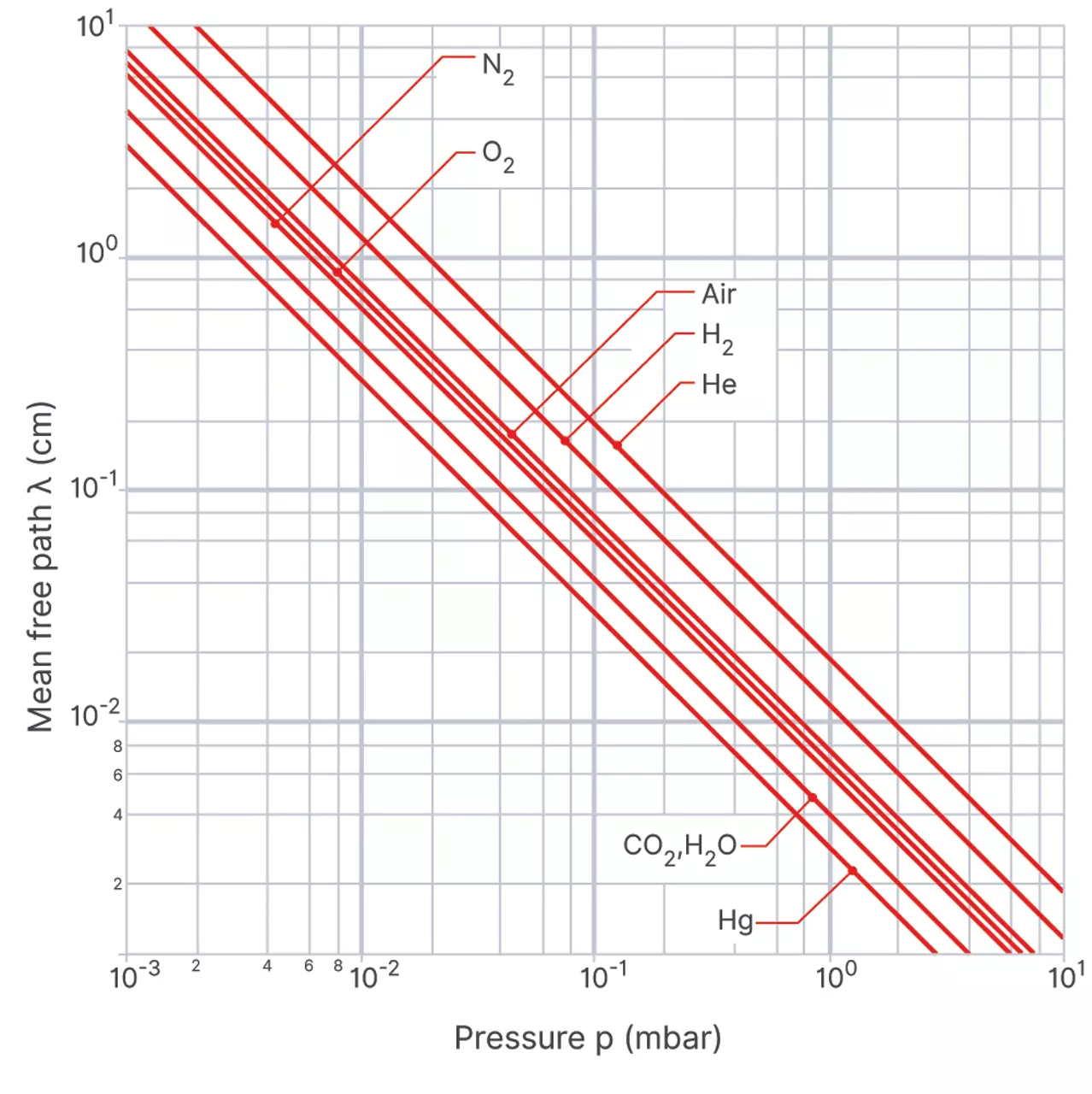
图 9.1 各种气体的平均自由程 λ (cm) 随压力的变化
表 3 使用平均自由程 λ 的乘积 c* 计算出的平均自由程 I 值
(以及 68°F 或 20°C 下各种气体的压力 p)(另见图 9.1)

表 4 气体运动理论重要公式汇总表
碰撞速率 zA(cm–2 ⋅ s–1) 和单层形成时间 τ (s)
在高真空状态下,常用的压力状态表征方法为计算在无气体的表面上形成单分子或单原子层所需的时间,并假设每个分子都会粘附到该表面上。这种单层形成时间与碰撞速率 zA 密切相关。气体静止时,碰撞速率会指示单位时间和表面积上与真空容器内表面发生碰撞的分子数量:
Leybold - Vacuum Fundamentals graphics
(1.20)
如果 a 表示每个单位表面积上可以容纳特定气体的间隙数,则单层形成时间为
Leybold - Vacuum Fundamentals graphics
(1.21)
碰撞频率 zv (cm–3 · s–1)
此为碰撞速率 z 和粒子数密度 n 的一半的乘积,因为两个分子的相互碰撞只计为一次碰撞:
Leybold - Vacuum Fundamentals graphics
(1.21a)




